Some time ago I was preparing for my ATPL theory exams, and, of course, I was making notes. Here are some of them, probably they could be helpful for someone.
First of all, I wrote down how many questions each subject contains, and the exams duration. Here they are:
- Air Law: 44 questions, 1 hour;
- Aircraft General Knowledge (Airframe, Systems Engines and Electrics): 80 questions, 2 hours;
- Instrumentation: 60 questions, 2 hours;
- Mass and Balance: 25 questions, 1 hour;
- Performance: 35 questions, 1 hour;
- Flight Planning and Monitoring: 43 questions, 2 hours;
- Human Performance and Limitations: 48 questions, 1 hour;
- Meteorology: 84 questions, 2 hours;
- General Navigation: 60 questions, 2 hours;
- Radio Navigation: 66 questions, 1 hour 30 minutes;
- Operational Procedures: 45 questions, 1 hour 15 minutes;
- Principles of Flight: 44 questions, 1 hour;
- VFR Communications: 24 questions, 30 minutes;
- IFR Communications: 24 questions, 30 minutes.
Each one has some difficulties, but some of them became my personal nightmares. For example, Air Law, Operation Procedures and General Navigation. The first two did because of huge amount of information to memorize, and the latter is because of timing: a lot of computations with only about 2 minutes per question.
Personal Experience with The Exams
- All posts about ATPL preparation and exams experience
- Obtaining the First Class Medical in Poland
- My favorite EASA question bank
- Enrolling into a Polish flight school theoretical course
- Theoretical course completion
- Exams booking in Czech Republic
- Passing IFR Communications
- Passing VFR Communications, Air Law, Mass and Balance, Operational Procedures and General Navigation
- Passing Aircraft General Knowledge, Radio Communications, Principles of Flight, Performance and Human Performance and Limitations
- Passing the rest of the exams: Meteorology, Instrumentation, Flight Planning and Monitoring
A lot of subjects mainly require knowledge. The only way to pass is reading the books. But some of them, for example, navigation, allow to solve a huge part of questions only by knowing a proper method. That’s why I decided to start this page with navigation problems.
General Navigation
Imagine that we have the following problem:
Course required: 085° (T)
Forecast W/V: 030/100 kt
TAS: 470 kt
Distance: 265 NM
Probably we can use a flight computer, but I do not prefer it in this kind of tasks because it can be solved with a simple sketch and 2-3 formulae. So, firstly let’s draw it:
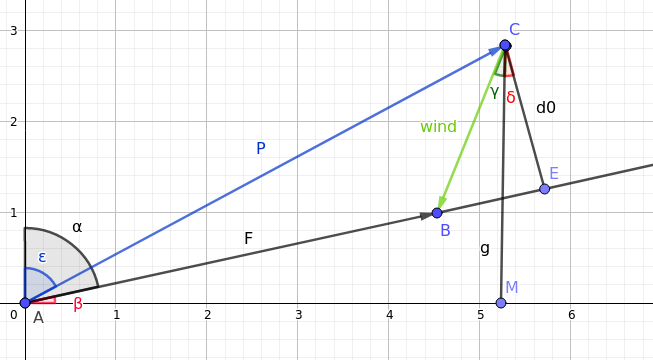
I did not do it in scale, but it does not matter for computation. We have our final track α (black angle around A, 85°). Wind angle is γ (green angle around point C, 30°), and wind speed is CB (green arrow). We also know AC (470 knots, it’s our speed vector without wind correction). We have to find AB (final speed value after wind correction) and ε, angle between AC and vertical axis (which is our required HDG).
We can see that δ = β = 90° – 85° = 5° (CM ⊥ AM, CE ⊥ AE so δ = β).
CE = wind * cos(γ + δ)
sin(α – ε) = CE / AC, so
ε = α – arcsin(CE / AC) = α – arcsin(wind * cos(γ + δ) / AC)
ε = 85° – arcsin(100° * cos(30° + 5°) / 470) = 75°
Now let’s find AB:
AB = AE – BE
AE = AC * cos(α – ε)
BE = wind * sin(γ + δ)
AB = AE – BE = AC * cos(α – ε) – wind * sin(γ + δ) =
470 * cos(85° – 75°) – 100 * sin(30° + 5°) = 405
Flight time is dist / speed = 265 / 405 = 0.654 h = 39 minutes.
Meteorology
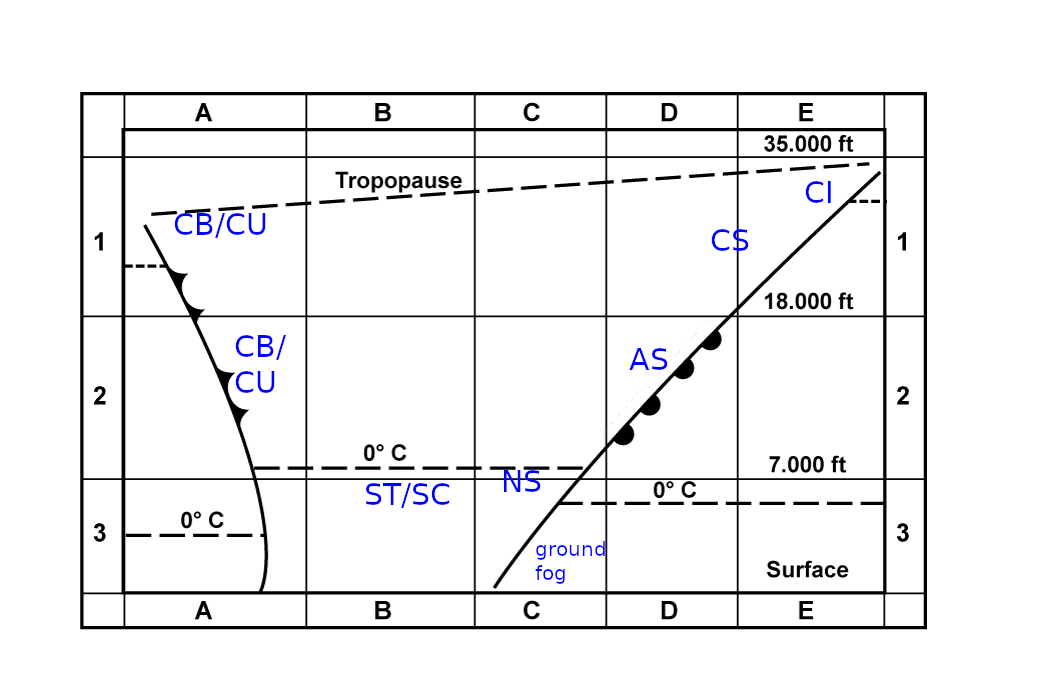
That picture helps me a lot in solving questions like “which cloud types are expected in sector …”.